TRIGOMETRIA I

CIRCULO TRIGONOMETRICO O UNITARIO

Ángulo y círculo trigonométrico o unitario

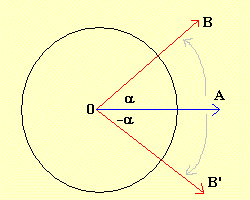
Ángulo trigonométrico:        Supongamos el rayo 0A fijo y el rayo 0B móvil. Comenzamos con los dos rayos coincidiendo. Ahora, hagamos girar 0B alrededor de 0. En cada posición de giro, 0B determina un ángulo con 0A: el ángulo A0B. Se ha convenido considerar los ángulos generados en sentido contrario a las manecillas del reloj como positivos, y a los generados en el mismo sentido de las manecillas del reloj como negativos: de acuerdo con la ilustración de la derecha (Fig.1), el ángulo A0B es positivo y el ángulo A0B' es negativo. Antes de iniciar el giro, los rayos 0A y 0B coinciden, formando un ángulo de 0° (en el sistema sexagesimal). Al girar 0B, en sentido contrario a las manecillas del reloj, irá generando un ángulo cada vez mayor y cuando vuelva a coincidir 0B con 0A se habrá efectuado un giro completo, generándose un ángulo giro cuya medida es de 360°. 0B puede continuar girando y engendrar un ángulo de cualquier medida; de lo anterior se deduce que 0A y 0B son los lados inicial y terminal, respectivamente, de una infinidad de ángulos.    Unidad de medida de los ángulos: los ángulos se expresan en grados sexagesimales, grados centesimales o en radianes.

(Fig.1)   (Fig.2)

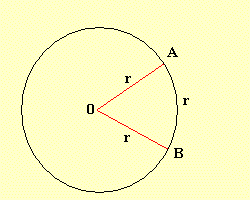
En el sistema sexagesimal se considera a la circunferencia dividida en 360 partes iguales; y un ángulo de 1° sexagesimal es la medida de aquel que se genera cuando el giro, en el mismo sentido de las manecillas del reloj, del lado terminal es de 1/360 parte de una vuelta completa. Cada grado se considera dividido en 60 partes iguales llamadas minutos y cada minuto en 60 partes iguales llamadas segundos. Los símbolos para estas unidades son: grado      ° minuto     '       segundo  ''

 Radián: un radián se define como la medida de un ángulo central que subtiende un arco con la misma longitud del radio de la circunferncia. En la (Fig.2), la longitud del radio r es igual a la del arco AB; el ángulo A0B mide 1p radianes.

 

En el sistema circular se utiliza como unidad de medida el "radián".

 Equivalencia de un ángulo en el sistema sexagesimal al circular y viceversa.

   Para medir los ángulos, los sistemas más utilizados son el sexagesimal y el circular. Es conveniente saber convertir un ángulo dado de un sistema a otro.

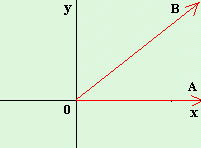
Ángulo en posición normal: Se dice que un ángulo está en posición normal cuando su lado inicial coincide con el semieje positivo de las abscisas en un sistema rectangular de ejes coordenados (Plano Cartesiano). Y cuyo vértice está en el origen de coordenadas (punto donde se intersectan los ejes). En la figura de la derecha se ilustra un ángulo en posición normal, el ángulo A0B.

 Círculo trigonométrico:

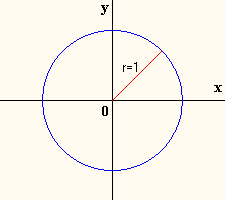
Se llama círculo trigonométrico, o goniométrico, a aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad. A la derecha se puede observar un círculo trigonométrico.

Veamos ahora unos  videos que nos clarifique un poco la cuestión......

   

Definicion de funciones trigonometricas en el circulo:

Comportamiento de las funciones segun el cuadrante




Radianes y  Grados 




Conversiones de un sistema a otro

SIGNO DE LAS FUNCIONES TRIGONOMETRICAS SEGUN EL CUADRANTE

                                                   

¡Veamos un video explicativo¡