Una ecuación diferencial de primer orden
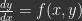
 (2)
(2)

son ejemplos de ecuaciones de variables separables. En el primer caso
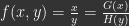 con
con  y
y  ; mientras que en el segundo
; mientras que en el segundo
 con
con  y
y 
 ,
,  no son ecuaciones de variables separables.
no son ecuaciones de variables separables.
Ahora veamos como se resuelve una ecuación diferencial de variables separables o separadas.
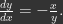
Observemos que es una ecuación de variables separables. En este ejemplo, La ecuación diferencial puede reescribirse como
La ecuación diferencial puede reescribirse como

y al integrar esta igualdad obtenemos , de donde
, de donde
 o equivalentemente
o equivalentemente
 Esta ecuación representa a una familia de soluciones, cuyos elementos son todas las circunferencias centradas en el origen.
Esta ecuación representa a una familia de soluciones, cuyos elementos son todas las circunferencias centradas en el origen.

Dicha ecuación la podemos reescribir como

o, equivalentemente
 .
.
De la expresión anterior vemos que y
y 
Para resolverla, la reescribimos como
 ,
,
y posteriormente procedemos a integrar esta igualdad
 ,
,
la primera integral es simple
 ,
,
mientas que la segunda integral se calcula mendiante integración por
se calcula mendiante integración por
partes: , tomando
, tomando  , por lo que
, por lo que
 . De esta forma,
. De esta forma,
 ,
por lo que, al igualar ambas integrales, obtenemos
,
por lo que, al igualar ambas integrales, obtenemos

En consecuancia, la solución se expresa implícitamente por

Aún cuando las ecuaciones de variables separables no son complicadas en su solución (las complicaciones que surgen se deben a la misma dificultad de las integrales involucradas), son un ejemplo del tipo de ecuaciones diferenciales que modelan problemas de muy distinta índole, que van del decaimiento radiactivo, a la dinámica de poblaciones en sus modelos malthusiano y logístico, problemas de enfriamiento y transmisión de enfermedades, entre otros. Algunos ejemplos de este tipo de modelos los puede encontrar el lector en la sección
Modelado y solucion de ecuaciones diferenciales de primer orden
(1)
se dice que es una ecuación de variables separables o con variables separadas si tiene la formaEjemplo 1
Las ecuaciones diferencialesson ejemplos de ecuaciones de variables separables. En el primer caso
Ejemplo 2
Las ecuaciones diferencialesAhora veamos como se resuelve una ecuación diferencial de variables separables o separadas.
Ejemplo 3
Consideremos la ecuación diferencialObservemos que es una ecuación de variables separables. En este ejemplo,
y al integrar esta igualdad obtenemos
Ejemplo 4
Resolver la ecuación diferencialDicha ecuación la podemos reescribir como
o, equivalentemente
De la expresión anterior vemos que
Para resolverla, la reescribimos como
y posteriormente procedemos a integrar esta igualdad
la primera integral es simple
mientas que la segunda integral
partes:
En consecuancia, la solución se expresa implícitamente por
Aún cuando las ecuaciones de variables separables no son complicadas en su solución (las complicaciones que surgen se deben a la misma dificultad de las integrales involucradas), son un ejemplo del tipo de ecuaciones diferenciales que modelan problemas de muy distinta índole, que van del decaimiento radiactivo, a la dinámica de poblaciones en sus modelos malthusiano y logístico, problemas de enfriamiento y transmisión de enfermedades, entre otros. Algunos ejemplos de este tipo de modelos los puede encontrar el lector en la sección
Modelado y solucion de ecuaciones diferenciales de primer orden

No hay comentarios:
Publicar un comentario